Pythonでのカメラ使用のプログラムはWindowsのスタンドアローン環境で動かす必要があると話していましたが、改めて調べるとGoogle Colaboratory上でも動作することが分かりました。
Google Colab (https://colab.research.google.com/ )からノートブックを新規作成で開いて、左端のメニューアイコンの下から「<>」となっているスニペットを選びます。今度は、右端にプログラムの処理のひな型(スニペット)の一覧が出てくるので、ここから「Camera Capture」のスニペットを選んで「挿入」を押すと、Google Colab上にセルが2個挿入されて、始めのセルで take_photo() という関数を設定して、その次のセルで実際にtake_photo()を使ってカメラ画像を1枚撮影してファイルに保存する処理が実行されます。(試すだけならすぐに作業できるので、もし時間があれば動作を確認してみて下さい。)
この処理のtake_photo()は以下のようになっています。
def take_photo(filename='photo.jpg', quality=0.8):
js = Javascript('''
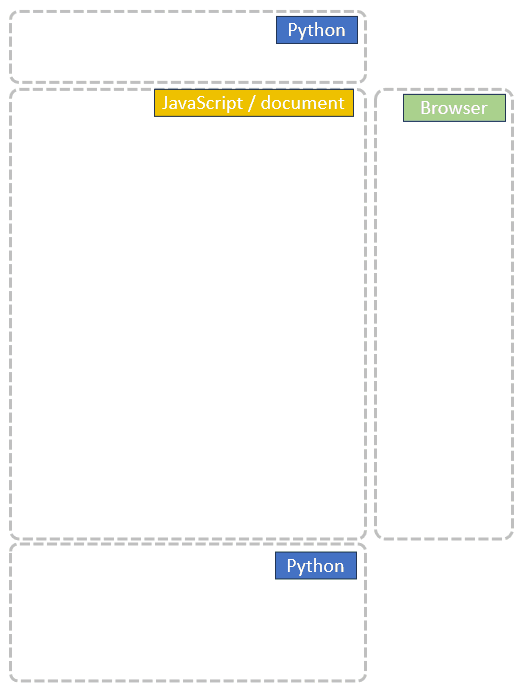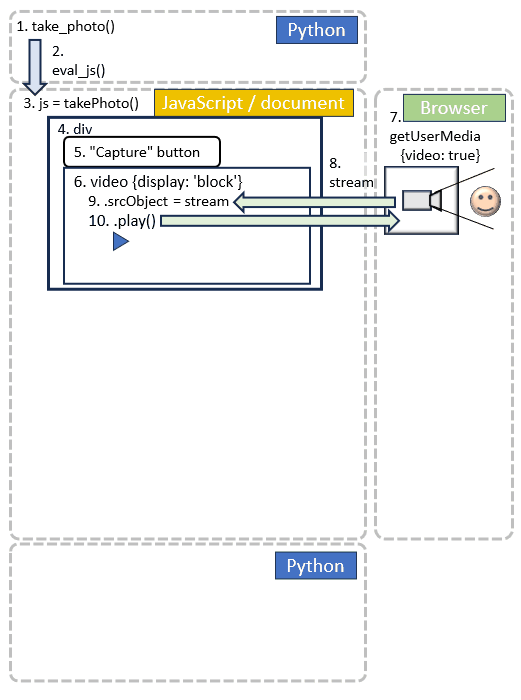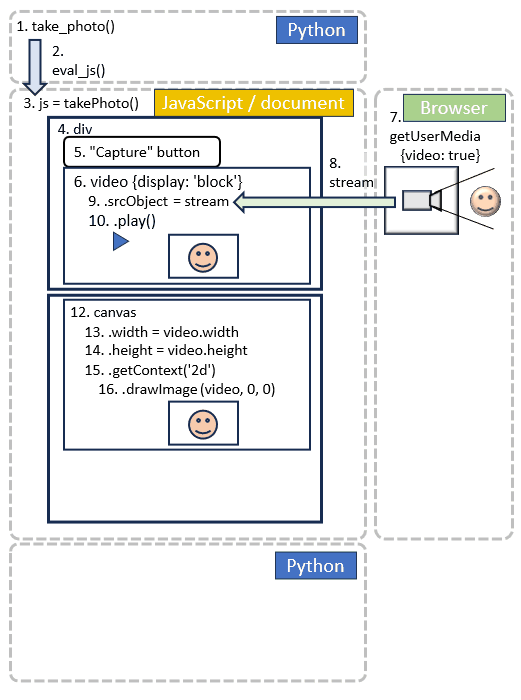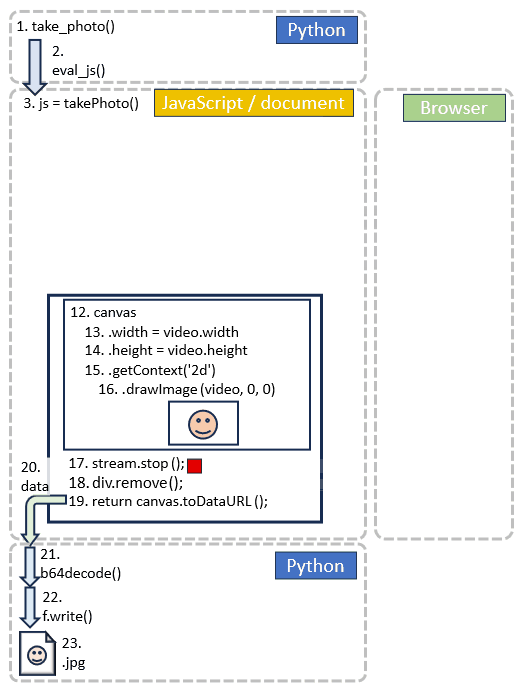
async function takePhoto(quality) {
const div = document.createElement('div');
const capture = document.createElement('button');
capture.textContent = 'Capture';
div.appendChild(capture);
const video = document.createElement('video');
video.style.display = 'block';
const stream = await navigator.mediaDevices.getUserMedia({video: true});
document.body.appendChild(div);
div.appendChild(video);
video.srcObject = stream;
await video.play();
// Resize the output to fit the video element.
google.colab.output.setIframeHeight(document.documentElement.scrollHeight, true);
// Wait for Capture to be clicked.
await new Promise((resolve) => capture.onclick = resolve);
const canvas = document.createElement('canvas');
canvas.width = video.videoWidth;
canvas.height = video.videoHeight;
canvas.getContext('2d').drawImage(video, 0, 0);
stream.getVideoTracks()[0].stop();
div.remove();
return canvas.toDataURL('image/jpeg', quality);
}
''')
display(js)
data = eval_js('takePhoto({})'.format(quality))
binary = b64decode(data.split(',')[1])
with open(filename, 'wb') as f:
f.write(binary)
return filename
}これはPythonのプログラムなのですが、「js = Javascript(...)」となって、カメラ処理の実体はウェブブラウザ側のJavaScriptで処理されていました。
それはともかく、これでGoogle Colabでカメラが使用できそうなので、Google側のGPUを使った処理も検討できるかもしれません。
上記のスニペットは1枚画像を撮影するだけですが、連続的に処理することも可能です(ただし、当然ながらJavaScriptもそこそこ分かっていないと作業できません)。
参考)
- Google Colaboratory で手元のカメラを使う(Google Colaboratory 提供のスニペットを使用)福山大金子研
- colaboratory上でWEBカメラを使用する
- Colaboratoryで、ループ処理内のカメラ映像を使用する方法
- Google Colaboratoryで外付けカメラを使う #Python – Qiita
Windows上Anaconda環境でOpenGLを動かす。
作業用に新環境を構築(Anaconda3のメニューからコマンドプロンプトを起動後に下記を実行)
(base) C:\Users\oshiro>conda create -n opengl
Collecting package metadata (current_repodata.json): done
Solving environment: done
## Package Plan ##
environment location: C:\Users\oshiro\Anaconda3\envs\opengl
Proceed ([y]/n)? y
Preparing transaction: done
Verifying transaction: done
Executing transaction: done
#
# To activate this environment, use
#
# $ conda activate opengl
#
# To deactivate an active environment, use
#
# $ conda deactivate
環境をアクティベート
(base) C:\Users\oshiro>conda activate opengl
(opengl) C:\Users\oshiro>
PyOpenGLパッケージのインストール(Anacondaでの指定はpyopengl)
(opengl) C:\Users\oshiro>conda install pyopengl
Collecting package metadata (current_repodata.json): done
Solving environment: done
## Package Plan ##
environment location: C:\Users\oshiro\Anaconda3\envs\opengl
added / updated specs:
- pyopengl
The following NEW packages will be INSTALLED:
ca-certificates pkgs/main/win-64::ca-certificates-2021.1.19-haa95532_0
certifi pkgs/main/win-64::certifi-2020.12.5-py38haa95532_0
openssl pkgs/main/win-64::openssl-1.1.1i-h2bbff1b_0
pip pkgs/main/win-64::pip-20.3.3-py38haa95532_0
pyopengl pkgs/main/win-64::pyopengl-3.1.1a1-py38_0
python pkgs/main/win-64::python-3.8.5-h5fd99cc_1
setuptools pkgs/main/win-64::setuptools-52.0.0-py38haa95532_0
sqlite pkgs/main/win-64::sqlite-3.33.0-h2a8f88b_0
vc pkgs/main/win-64::vc-14.2-h21ff451_1
vs2015_runtime pkgs/main/win-64::vs2015_runtime-14.27.29016-h5e58377_2
wheel pkgs/main/noarch::wheel-0.36.2-pyhd3eb1b0_0
wincertstore pkgs/main/win-64::wincertstore-0.2-py38_0
zlib pkgs/main/win-64::zlib-1.2.11-h62dcd97_4
Proceed ([y]/n)? y
Preparing transaction: done
Verifying transaction: done
Executing transaction: done(PyOpenGL-Demoもあるが、こちらはcondaからは直接インストールできないみたい。pipで環境を壊すと困るので、とりあえず保留)
Pythonは3.8.5となっている
(opengl) C:\Users\oshiro>python -V
Python 3.8.5
さらに、Spyder, Jupyter Notebook, NumPy, Matplotlib, Pillow 等々を使いたいので、まとめて anaconda パッケージでインストール。
(opengl) C:\Users\oshiro>conda install anaconda
Collecting package metadata (current_repodata.json): done
Solving environment: failed with initial frozen solve. Retrying with flexible solve.
Solving environment: failed with repodata from current_repodata.json, will retry with next repodata source.
Collecting package metadata (repodata.json): done
Solving environment: done
## Package Plan ##
environment location: C:\Users\oshiro\Anaconda3\envs\opengl
added / updated specs:
- anaconda
The following packages will be downloaded:
package | build
---------------------------|-----------------
_anaconda_depends-2020.07 | py38_0 6 KB
alabaster-0.7.12 | pyhd3eb1b0_0 16 KB
anaconda-custom | py38_1 36 KB
anaconda-client-1.7.2 | py38_0 172 KB
anaconda-project-0.9.1 | pyhd3eb1b0_1 215 KB
argh-0.26.2 | py38_0 36 KB
argon2-cffi-20.1.0 | py38he774522_1 50 KB
astroid-2.4.2 | py38_0 295 KB
astropy-4.2 | py38h2bbff1b_0 5.9 MB
async_generator-1.10 | pyhd3eb1b0_0 23 KB
backcall-0.2.0 | pyhd3eb1b0_0 13 KB
bcrypt-3.2.0 | py38he774522_0 44 KB
beautifulsoup4-4.9.3 | pyha847dfd_0 86 KB
bitarray-1.6.3 | py38h2bbff1b_1 95 KB
bkcharts-0.2 | py38_0 133 KB
bleach-3.3.0 | pyhd3eb1b0_0 113 KB
bokeh-2.2.3 | py38_0 5.4 MB
boto-2.49.0 | py38_0 1.2 MB
bottleneck-1.3.2 | py38h2a96729_1 106 KB
brotlipy-0.7.0 |py38h2bbff1b_1003 412 KB
cffi-1.14.4 | py38hcd4344a_0 245 KB
chardet-4.0.0 |py38haa95532_1003 211 KB
click-7.1.2 | pyhd3eb1b0_0 64 KB
clyent-1.2.2 | py38_1 20 KB
comtypes-1.1.8 |py38haa95532_1002 236 KB
cryptography-3.3.1 | py38hcd4344a_0 610 KB
cycler-0.10.0 | py38_0 14 KB
cython-0.29.21 | py38hd77b12b_0 1.8 MB
cytoolz-0.11.0 | py38he774522_0 289 KB
dask-2021.1.1 | pyhd3eb1b0_0 5 KB
dask-core-2021.1.1 | pyhd3eb1b0_0 636 KB
decorator-4.4.2 | pyhd3eb1b0_0 12 KB
distributed-2021.1.1 | py38haa95532_1 1.0 MB
docutils-0.16 | py38_1 668 KB
entrypoints-0.3 | py38_0 11 KB
fastcache-1.1.0 | py38he774522_0 31 KB
filelock-3.0.12 | pyhd3eb1b0_1 10 KB
flask-1.1.2 | pyhd3eb1b0_0 70 KB
future-0.18.2 | py38_1 649 KB
gevent-21.1.1 | py38h2bbff1b_1 1.4 MB
glob2-0.7 | pyhd3eb1b0_0 12 KB
gmpy2-2.0.8 | py38h7edee0f_3 145 KB
greenlet-1.0.0 | py38hd77b12b_2 82 KB
h5py-2.10.0 | py38h5e291fa_0 841 KB
idna-2.10 | pyhd3eb1b0_0 52 KB
imagecodecs-2021.1.11 | py38h5da4933_1 5.9 MB
imagesize-1.2.0 | pyhd3eb1b0_0 8 KB
iniconfig-1.1.1 | pyhd3eb1b0_0 8 KB
ipykernel-5.3.4 | py38h5ca1d4c_0 182 KB
ipython-7.20.0 | py38hd4e2768_1 1012 KB
ipywidgets-7.6.3 | pyhd3eb1b0_1 105 KB
isort-5.7.0 | pyhd3eb1b0_0 82 KB
itsdangerous-1.1.0 | pyhd3eb1b0_0 17 KB
jedi-0.17.2 | py38haa95532_1 921 KB
jinja2-2.11.3 | pyhd3eb1b0_0 101 KB
jupyter-1.0.0 | py38_7 8 KB
jupyter_core-4.7.1 | py38haa95532_0 85 KB
jupyterlab_widgets-1.0.0 | pyhd3eb1b0_1 109 KB
keyring-22.0.1 | py38haa95532_0 70 KB
kiwisolver-1.3.1 | py38hd77b12b_0 52 KB
lazy-object-proxy-1.4.3 | py38h2bbff1b_2 31 KB
lerc-2.2.1 | hd77b12b_0 114 KB
libdeflate-1.7 | h2bbff1b_5 49 KB
llvmlite-0.34.0 | py38h1a82afc_4 12.4 MB
locket-0.2.1 | py38haa95532_1 10 KB
lxml-4.6.2 | py38h9b66d53_0 979 KB
lz4-c-1.9.3 | h2bbff1b_0 131 KB
markupsafe-1.1.1 | py38he774522_0 29 KB
matplotlib-base-3.3.2 | py38hba9282a_0 5.1 MB
mccabe-0.6.1 | py38_1 15 KB
menuinst-1.4.16 | py38he774522_1 269 KB
mistune-0.8.4 |py38he774522_1000 55 KB
mkl-service-2.3.0 | py38h196d8e1_0 47 KB
mkl_fft-1.2.0 | py38h45dec08_0 122 KB
mkl_random-1.1.1 | py38h47e9c7a_0 245 KB
mpmath-1.1.0 | py38_0 777 KB
msgpack-python-1.0.2 | py38h59b6b97_1 76 KB
multipledispatch-0.6.0 | py38_0 23 KB
mypy_extensions-0.4.3 | py38_0 10 KB
nbconvert-6.0.7 | py38_0 500 KB
nbformat-5.1.2 | pyhd3eb1b0_1 68 KB
notebook-6.2.0 | py38haa95532_0 4.4 MB
numba-0.51.2 | py38hf9181ef_1 3.1 MB
numexpr-2.7.2 | py38hcbcaa1e_0 123 KB
numpy-1.19.2 | py38hadc3359_0 22 KB
numpy-base-1.19.2 | py38ha3acd2a_0 3.8 MB
olefile-0.46 | py_0 33 KB
openpyxl-3.0.6 | pyhd3eb1b0_0 159 KB
packaging-20.9 | pyhd3eb1b0_0 37 KB
pandas-1.2.1 | py38hf11a4ad_0 7.9 MB
pandocfilters-1.4.3 | py38haa95532_1 14 KB
path-15.1.0 | py38haa95532_0 37 KB
pathlib2-2.3.5 | py38haa95532_2 62 KB
patsy-0.5.1 | py38_0 274 KB
pep8-1.7.1 | py38_0 69 KB
pillow-8.1.0 | py38h4fa10fc_0 664 KB
pkginfo-1.7.0 | py38haa95532_0 60 KB
pluggy-0.13.1 | py38_0 34 KB
ply-3.11 | py38_0 81 KB
psutil-5.8.0 | py38h2bbff1b_1 350 KB
ptyprocess-0.7.0 | pyhd3eb1b0_2 17 KB
py-lief-0.10.1 | py38ha925a31_0 1.1 MB
pycosat-0.6.3 | py38h2bbff1b_0 75 KB
pycurl-7.43.0.6 | py38h7a1dbc1_0 65 KB
pyerfa-1.7.1.1 | py38h2bbff1b_1 341 KB
pyflakes-2.2.0 | pyhd3eb1b0_0 56 KB
pygments-2.7.4 | pyhd3eb1b0_0 676 KB
pylint-2.6.0 | py38_0 462 KB
pynacl-1.4.0 | py38h62dcd97_1 1.2 MB
pyodbc-4.0.30 | py38ha925a31_0 68 KB
pyparsing-2.4.7 | pyhd3eb1b0_0 59 KB
pyqt-5.9.2 | py38ha925a31_4 3.2 MB
pyreadline-2.1 | py38_1 145 KB
pyrsistent-0.17.3 | py38he774522_0 92 KB
pysocks-1.7.1 | py38haa95532_0 31 KB
pytables-3.6.1 | py38ha5be198_0 1.1 MB
pytest-6.2.2 | py38haa95532_2 458 KB
python-dateutil-2.8.1 | pyhd3eb1b0_0 221 KB
python-libarchive-c-2.9 | pyhd3eb1b0_0 46 KB
pytz-2021.1 | pyhd3eb1b0_0 181 KB
pywavelets-1.1.1 | py38he774522_2 3.4 MB
pywin32-227 | py38he774522_1 5.6 MB
pywin32-ctypes-0.2.0 | py38_1000 42 KB
pywinpty-0.5.7 | py38_0 52 KB
pyyaml-5.4.1 | py38h2bbff1b_1 151 KB
pyzmq-20.0.0 | py38hd77b12b_1 405 KB
qtconsole-5.0.2 | pyhd3eb1b0_0 97 KB
regex-2020.11.13 | py38h2bbff1b_0 324 KB
rtree-0.9.4 | py38h21ff451_1 49 KB
ruamel_yaml-0.15.87 | py38he774522_1 264 KB
scikit-image-0.17.2 | py38h1e1f486_0 8.9 MB
scikit-learn-0.23.2 | py38h47e9c7a_0 4.7 MB
scipy-1.6.0 | py38h14eb087_0 13.0 MB
simplegeneric-0.8.1 | py38_2 10 KB
sip-4.19.13 | py38ha925a31_0 262 KB
six-1.15.0 | py38haa95532_0 27 KB
snowballstemmer-2.1.0 | pyhd3eb1b0_0 62 KB
sortedcollections-2.1.0 | pyhd3eb1b0_0 12 KB
sphinx-3.4.3 | pyhd3eb1b0_0 1.1 MB
sphinxcontrib-1.0 | py38_1 4 KB
sphinxcontrib-applehelp-1.0.2| pyhd3eb1b0_0 29 KB
sphinxcontrib-devhelp-1.0.2| pyhd3eb1b0_0 23 KB
sphinxcontrib-htmlhelp-1.0.3| pyhd3eb1b0_0 28 KB
sphinxcontrib-jsmath-1.0.1 | pyhd3eb1b0_0 8 KB
sphinxcontrib-qthelp-1.0.3 | pyhd3eb1b0_0 26 KB
sphinxcontrib-serializinghtml-1.1.4| pyhd3eb1b0_0 24 KB
spyder-4.2.1 | py38haa95532_1 5.7 MB
spyder-kernels-1.10.1 | py38haa95532_0 100 KB
sqlalchemy-1.3.23 | py38h2bbff1b_0 1.5 MB
statsmodels-0.12.1 | py38h2bbff1b_0 8.2 MB
sympy-1.7.1 | py38haa95532_0 8.8 MB
terminado-0.9.2 | py38haa95532_0 26 KB
testpath-0.4.4 | pyhd3eb1b0_0 85 KB
textdistance-4.2.1 | pyhd3eb1b0_0 29 KB
tifffile-2021.1.14 | pyhd3eb1b0_1 126 KB
toolz-0.11.1 | pyhd3eb1b0_0 46 KB
tornado-6.1 | py38h2bbff1b_0 612 KB
tqdm-4.56.0 | pyhd3eb1b0_0 80 KB
traitlets-5.0.5 | pyhd3eb1b0_0 81 KB
typed-ast-1.4.2 | py38h2bbff1b_1 139 KB
typing_extensions-3.7.4.3 | pyh06a4308_0 28 KB
ujson-4.0.2 | py38hd77b12b_0 46 KB
unicodecsv-0.14.1 | py38_0 28 KB
urllib3-1.26.3 | pyhd3eb1b0_0 105 KB
watchdog-1.0.2 | py38haa95532_1 104 KB
webencodings-0.5.1 | py38_1 20 KB
werkzeug-1.0.1 | pyhd3eb1b0_0 239 KB
widgetsnbextension-3.5.1 | py38_0 863 KB
win_inet_pton-1.1.0 | py38haa95532_0 35 KB
win_unicode_console-0.5 | py38_0 34 KB
wrapt-1.11.2 | py38he774522_0 46 KB
xlsxwriter-1.3.7 | pyhd3eb1b0_0 105 KB
xlwings-0.22.0 | py38haa95532_0 816 KB
xlwt-1.3.0 | py38_0 160 KB
zfp-0.5.5 | hd77b12b_4 134 KB
zict-2.0.0 | pyhd3eb1b0_0 10 KB
zope-1.0 | py38_1 5 KB
zope.event-4.5.0 | py38_0 210 KB
zope.interface-5.2.0 | py38h2bbff1b_0 307 KB
------------------------------------------------------------
Total: 150.8 MB
The following NEW packages will be INSTALLED:
_anaconda_depends pkgs/main/win-64::_anaconda_depends-2020.07-py38_0
alabaster pkgs/main/noarch::alabaster-0.7.12-pyhd3eb1b0_0
anaconda pkgs/main/win-64::anaconda-custom-py38_1
anaconda-client pkgs/main/win-64::anaconda-client-1.7.2-py38_0
anaconda-project pkgs/main/noarch::anaconda-project-0.9.1-pyhd3eb1b0_1
(略)
Proceed ([y]/n)? y
Downloading and Extracting Packages
rtree-0.9.4 | 49 KB | ####################### | 100%
pywin32-227 | 5.6 MB | ####################### | 100%
(略)
Preparing transaction: done
Verifying transaction: done
Executing transaction:
(下記)
done「Extracting transaction:」後に下記のような「DEBUG menuinst_win32:…」が実行されて、これでWindowsメニュー向けのショートカットが作成されていた。
- DEBUG menuinst_win32:__init__(199): Menu: name: 'Anaconda${PY_VER} ${PLATFORM}', prefix: 'C:\Users\oshiro\Anaconda3\envs\opengl', env_name: 'opengl', mode: 'user', used_mode: 'user'
DEBUG menuinst_win32:create(323): Shortcut cmd is %windir%\System32\cmd.exe, args are ['"/K"', 'C:\\Users\\oshiro\\Anaconda3\\Scripts\\activate.bat', 'C:\\Users\\oshiro\\Anaconda3\\envs\\opengl']
\ DEBUG menuinst_win32:__init__(199): Menu: name: 'Anaconda${PY_VER} ${PLATFORM}', prefix: 'C:\Users\oshiro\Anaconda3\envs\opengl', env_name: 'opengl', mode: 'user', used_mode: 'user'
DEBUG menuinst_win32:create(323): Shortcut cmd is %windir%\System32\WindowsPowerShell\v1.0\powershell.exe, args are ['-ExecutionPolicy', 'ByPass', '-NoExit', '-Command', '"& \'C:\\Users\\oshiro\\Anaconda3\\shell\\condabin\\conda-hook.ps1\' ; conda activate \'C:\\Users\\oshiro\\Anaconda3\\envs\\opengl\' "']
DEBUG menuinst_win32:__init__(199): Menu: name: 'Anaconda${PY_VER} ${PLATFORM}', prefix: 'C:\Users\oshiro\Anaconda3\envs\opengl', env_name: 'opengl', mode: 'user', used_mode: 'user'
DEBUG menuinst_win32:create(323): Shortcut cmd is C:\Users\oshiro\Anaconda3\python.exe, args are ['C:\\Users\\oshiro\\Anaconda3\\cwp.py', 'C:\\Users\\oshiro\\Anaconda3\\envs\\opengl', 'C:\\Users\\oshiro\\Anaconda3\\envs\\opengl\\python.exe', 'C:\\Users\\oshiro\\Anaconda3\\envs\\opengl\\Scripts\\jupyter-notebook-script.py', '"%USERPROFILE%/"']
| DEBUG menuinst_win32:__init__(199): Menu: name: 'Anaconda${PY_VER} ${PLATFORM}', prefix: 'C:\Users\oshiro\Anaconda3\envs\opengl', env_name: 'opengl', mode: 'user', used_mode: 'user'
DEBUG menuinst_win32:create(323): Shortcut cmd is C:\Users\oshiro\Anaconda3\pythonw.exe, args are ['C:\\Users\\oshiro\\Anaconda3\\cwp.py', 'C:\\Users\\oshiro\\Anaconda3\\envs\\opengl', 'C:\\Users\\oshiro\\Anaconda3\\envs\\opengl\\pythonw.exe', 'C:\\Users\\oshiro\\Anaconda3\\envs\\opengl\\Scripts\\spyder-script.py']
DEBUG menuinst_win32:create(323): Shortcut cmd is C:\Users\oshiro\Anaconda3\python.exe, args are ['C:\\Users\\oshiro\\Anaconda3\\cwp.py', 'C:\\Users\\oshiro\\Anaconda3\\envs\\opengl', 'C:\\Users\\oshiro\\Anaconda3\\envs\\opengl\\python.exe', 'C:\\Users\\oshiro\\Anaconda3\\envs\\opengl\\Scripts\\spyder-script.py', '--reset'](また、GLUTではなく、今どきだとGLFWを使うほうがよいとの解説も見つかって、こちらもconda-forgeからインストールはできたものの、Anaconda側のPythonとバージョンが合わないのか、importしても「ModuleNotFoundError: No module named ‘glfw’」等のエラーになってしまった。)
実際の実行には FreeGLUTのバイナリライブラリが必要になる。インストールしていないと glutInit()の時点で下記のようなエラーが出る。
(opengl) C:\Users\oshiro>python opengl-sample.py
Traceback (most recent call last):
File "opengl-sample.py", line 6, in <module>
glutInit(sys.argv)
File "C:\Users\oshiro\Anaconda3\envs\opengl\lib\site-packages\OpenGL\GLUT\special.py", line 333, in glutInit
_base_glutInit( ctypes.byref(count), holder )
File "C:\Users\oshiro\Anaconda3\envs\opengl\lib\site-packages\OpenGL\platform\baseplatform.py", line 405, in __call__
raise error.NullFunctionError(
OpenGL.error.NullFunctionError: Attempt to call an undefined function glutInit, check for bool(glutInit) before calling下記リンクから、MSVC版を入手。
この.zipファイルを展開して、bin側のfreeglut\bin\x64\freeglut.dll を C:\Windows\System32\ へコピー(lib側のfreeglut\lib\x64\freeglut.libではないので注意!)。
↓.zipファイルのfreeglut.dllを
↓C:\Windows\System32へコピー
これで、下記のスクリプトでティーポットを表示できる(opengl-sample.py)。
import sys
from OpenGL.GL import *
from OpenGL.GLU import *
from OpenGL.GLUT import *
def display(): # 表示用
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT)
glMatrixMode(GL_MODELVIEW)
glLoadIdentity() # 変換行列初期化
gluLookAt(3.0, 4.0, 5.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0) # カメラ設定
glMaterialfv(GL_FRONT_AND_BACK, GL_AMBIENT_AND_DIFFUSE, (0.8, 0.0, 0.0, 1.0)) # 色付け
#glutSolidSphere(1.0, 32, 32) # 球(サイズ、分割数, 分割数)
#glutSolidTorus(0.25, 0.80, 32, 32) # トーラス(サイズ, 分割数, 分割数)
glutSolidTeapot(1.0) # ティーポット(サイズ)
glFlush() # 表示更新
def reshape(w, h): # 再描画設定
glMatrixMode(GL_PROJECTION)
glLoadIdentity()
gluPerspective(30.0, 1.0*w/h, 1.0, 100.0) # 透視投影設定
# GLUT初期設定
glutInit(sys.argv) # GLUT初期化
glutInitWindowSize(300, 300) # 表示ウィンドウのサイズ指定
glutInitWindowPosition(100, 100) # 表示ウィンドウの位置指定
glutCreateWindow(b"Hello") # 表示ウィンドウの生成(ウィンドウタイトルに指定する文字列指定はb"..."としないとダメ)
# コールバック関数の指定
glutDisplayFunc(display)
glutReshapeFunc(reshape)
# 3次元表示設定
glEnable(GL_DEPTH_TEST)
glEnable(GL_LIGHTING)
glEnable(GL_LIGHT0)
# GLUTイベント処理の開始(抜けるには glutLeaveMainLoop())
glutMainLoop()
GLUTに渡す文字列は b”…” 指定しないとエラーになる。例えば、glutCreateWindow()に指定するウィンドウタイトルを “Hello” のように指定すると下記の「<class ‘TypeError’>: wrong type」のようなエラーが出る。キー入力をイベントを扱う際にも、エスケープを b”\x33″ としたり、b”W” にしたりしないと正しく認識できないらしい。
(opengl) C:\Users\oshiro>python opengl-sample.py
Traceback (most recent call last):
File "opengl-sample.py", line 32, in <module>
glutCreateWindow("Hello")
File "C:\Users\oshiro\Anaconda3\envs\opengl\lib\site-packages\OpenGL\GLUT\special.py", line 73, in glutCreateWindow
return __glutCreateWindowWithExit(title, _exitfunc)
ctypes.ArgumentError: argument 1: <class 'TypeError'>: wrong typeそれから、Spyder上でGLUTを動かすと、IPythonとの兼ね合いなのかエラーメッセージが表示されなくなってしまうため、手間は掛かるがコマンドプロンプトを別で用意して実行した方がデバッグはしやすい。
リンク
なぜかこれまで動作していたアンドロイドアプリで、AndroidX絡みで「ERROR: This project uses AndroidX dependencies, but the ‘android.useAndroidX’ property is not enabled」と出るようになってしまった。
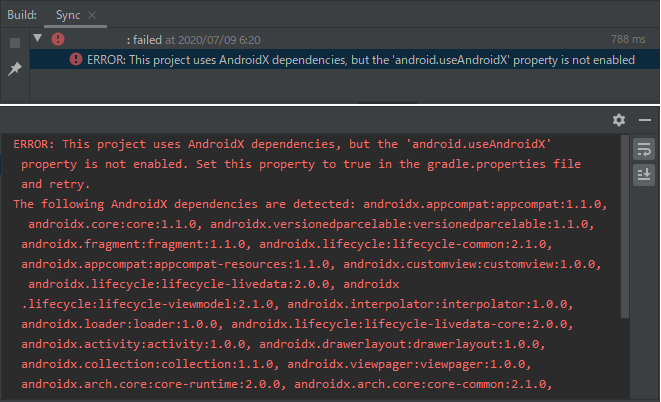
gradle.propertiesファイル内でこれを下記のように有効化しないといけなかった(いけなくなった?)らしい。
#gradle.properties
android.useAndroidX=true
android.enableJetifier=true
リンク
「行列」は縦と横のどれがどれかが分からなくなったら、横書きを基本にして、左から右に移動してそのまま字面のとおり、まずは「行」。
次に、右に移動したまま下に降ろすようなイメージで「列」。これだと忘れない。
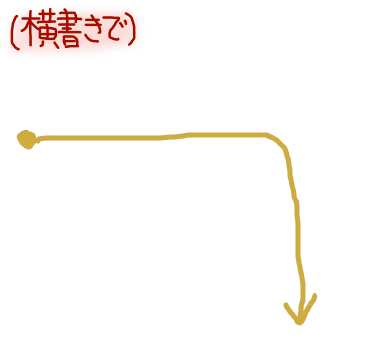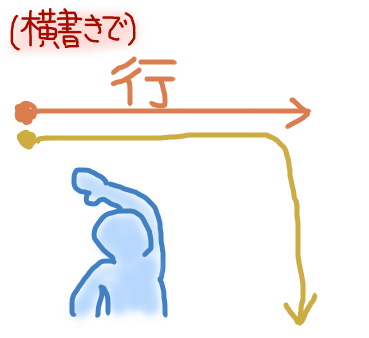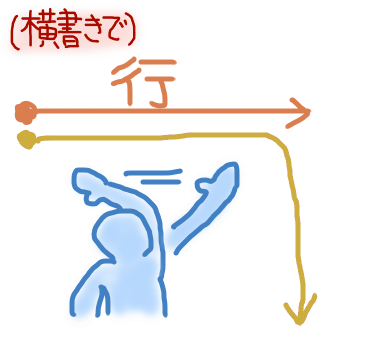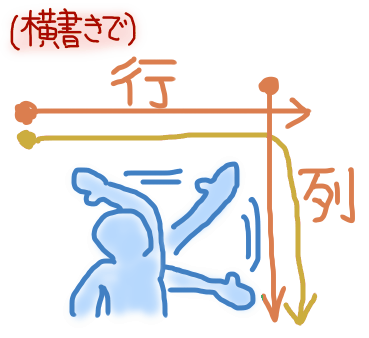
(行列の掛け算の際もこの形。$AB$の積で、$A$の行と$B$の列とを掛け合わせる。「行→」×「列↓」で求まる。要素の添え字も行,列の順序で、$i$行$j$列目の要素は$a_{ij}$となる。)
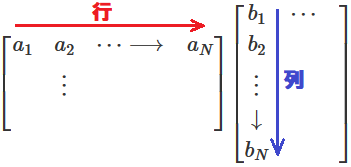

あとは、「列」だけで言うと、運動会でクラスごととかで並ばされているイメージ。

2020年7月5日 in
未分類 | tags:
行と列 |
No Comments
(関連記事:常用対数の近似値の算出)
対数は「$x$を何乗したら$z$になるか」を求めるものと捉える。
$z=x^y$での$y$を知りたい場合に$y=\log_{x}z$と書く。
$x$を底(base)、$z$を真数(anti-logarithm、逆対数)と呼ぶ。
底が10の場合を常用対数($\log_{10}$)。底が${\rm e}$の場合を自然対数(natural logarithm)と呼び、$\log_{\rm e}$を$\ln$とも書く。
公式
-
$z=x^y \Leftrightarrow y=\log_x z$,
-
$x^{\log_x z}=x^y=z$(冪の底と指数にある対数の底が同じ場合は、指数部の対数の真数のみに),
-
$\log_\underline{x} \underline{x}^y = \log_{x}z =y$(対数の底と真数の冪の底が同じ場合は、真数の指数に),
-
$x^1=x \Leftrightarrow \log_x x = 1$, $x^0=1 \Leftrightarrow \log_x 1 = 0$,
-
$z^p=(x^y)^p=\underbrace{x^y\cdot x^y\cdots x^y}_p=x^{\overbrace{y+y+\cdots+y}^p}=x^{py}$
$\Rightarrow\log_x z^p=\log_x {(x^y)}^p=\log_x x^{py}=py=p\log_x{z}$(真数の指数は係数に出せる)
-
$z_1=x^a, z_2=x^b; z_1z_2=x^ax^b=x^{a+b}$
$\Leftrightarrow$
$\log z_1z_2=\log x^ax^b=\log x^{a+b}$$=(a+b)\log x=a\log x + b\log x$$=\log x^a + \log x^b=\log z_1 + \log z_2$。
$\log z_1/z_2=\log x^ax^{-b}=\log x^{a-b}$$=(a-b)\log x=a\log x – b\log x$$=\log x^a – \log x^b=\log z_1 – \log z_2$。
(対数を取ると、乗除が加減算に)
-
$z=x^y$で両辺の対数を取ると、$\log_a z = \log_a x^y = y\log_a x \Rightarrow y = \displaystyle\frac{\log_a z}{\log_a x}$。
上式で、対数の底を$x$とすると$y = \displaystyle\frac{\log_x z}{\log_x x}=\displaystyle\frac{\log_x z}{1}=\log_x z$ $\Rightarrow \log_x z=\displaystyle\frac{\log_a z}{\log_a x}$ (対数の底の変換)
逆に、対数の底を$z$とすると、$y = \displaystyle\frac{\log_z z}{\log_z x}=\displaystyle\frac{1}{\log_z x}$ $\Rightarrow \log_x z=\displaystyle\frac{1}{\log_z x}$(底と真数の入れ替えで逆数に)
-
$\log_{x^p}z=\displaystyle\frac{\log_x z}{\log_x x^p}=\displaystyle\frac{\log_x z}{p\log_x x}=\displaystyle\frac{\log_x z}{p\cdot 1}=\displaystyle\frac{1}{p}\log_x z=\log_x z^\frac{1}{p}$(底の$p$乗は真数の$1/p$乗)
$\left(y=\log_{x^p}z\Leftrightarrow (x^p)^y=(x^y)^p=z\Rightarrow x^y=\sqrt[p]{z}=z^{\frac{1}{p}}\Leftrightarrow y=\log_x{z^{\frac{1}{p}}} \right)$
-
$\log_{x^p}z^p=\displaystyle\frac{\log_a z^p}{\log_a x^p}=\displaystyle\frac{\cancel{p}\log_a z}{\cancel{p}\log_a x}=\displaystyle\frac{\log_a z}{\log_a x}=\log_x z$(底と真数の$p$乗は相殺)
$\left(上式で底をxとして、\log_{x^p}z^p=\displaystyle\frac{\log_x z^p}{\log_x x^p}=\displaystyle\frac{\cancel{p}\log_x z}{\cancel{p}\log_x x}=\displaystyle\frac{\log_x z}{1}=\log_x z\right)$
$\left(z^p=(x^p)^y=(x^y)^p \Rightarrow \sqrt[p]{z^p}=\sqrt[p]{(x^y)^p} \Rightarrow z=x^y \right)$
-
$\log_a b\cdot \log_b c=\displaystyle\frac{\cancel{\log_x b}}{\log_x a}\displaystyle\frac{\log_x c}{\cancel{\log_x b}}=\displaystyle\frac{\log_x c}{\log_x a}=\log_a c$(真数と底の連鎖で相殺)
$\left(上式で底をaとして、\log_a b\cdot \log_b c=\cancel{\log_a b}\displaystyle\frac{\log_a c}{\cancel{\log_a b}}=\log_a c\right)$
-
常用対数から自然対数への変換 $\ln z=\displaystyle\frac{\log_{10}z}{\log_{10}{\rm e}}=\displaystyle\frac{\log_{10}z}{\log_{10}2.718\cdots}=\displaystyle\frac{\log_{10}z}{0.434\cdots}\fallingdotseq 2.3\log_{10}z$
2020年7月3日 in
未分類 | tags:
対数 |
No Comments








