Python-ControlをAnacondaへインストール。MATLAB互換機能がこんなに簡単にPythonで使えるようになっているとは思わなかった。
>conda install -c conda-forge control slycot
Collecting package metadata (current_repodata.json): done
Solving environment: done
## Package Plan ##
environment location: C:\Users\oshiro\Anaconda3
added / updated specs:
- control
- slycot
The following packages will be downloaded:
package | build
---------------------------|-----------------
ca-certificates-2020.4.5.2 | hecda079_0 184 KB conda-forge
certifi-2020.4.5.2 | py37hc8dfbb8_0 152 KB conda-forge
clangdev-5.0.0 | flang_3 189.0 MB conda-forge
conda-4.8.3 | py37hc8dfbb8_1 3.1 MB conda-forge
control-0.8.3 | py37_1 350 KB conda-forge
libblas-3.8.0 |8_h8933c1f_netlib 188 KB conda-forge
libcblas-3.8.0 |8_h8933c1f_netlib 88 KB conda-forge
libflang-5.0.0 |h6538335_20180525 519 KB conda-forge
liblapack-3.8.0 |8_h8933c1f_netlib 2.7 MB conda-forge
openmp-5.0.0 | vc14_0 576 KB conda-forge
python_abi-3.7 | 1_cp37m 4 KB conda-forge
slycot-0.4.0.0 | py37h9a9bad4_1 1.2 MB conda-forge
------------------------------------------------------------
Total: 198.0 MB
The following NEW packages will be INSTALLED:
clangdev conda-forge/win-64::clangdev-5.0.0-flang_3
control conda-forge/win-64::control-0.8.3-py37_1
libblas conda-forge/win-64::libblas-3.8.0-8_h8933c1f_netlib
libcblas conda-forge/win-64::libcblas-3.8.0-8_h8933c1f_netlib
libflang conda-forge/win-64::libflang-5.0.0-h6538335_20180525
liblapack conda-forge/win-64::liblapack-3.8.0-8_h8933c1f_netlib
openmp conda-forge/win-64::openmp-5.0.0-vc14_0
python_abi conda-forge/win-64::python_abi-3.7-1_cp37m
slycot conda-forge/win-64::slycot-0.4.0.0-py37h9a9bad4_1
The following packages will be UPDATED:
ca-certificates pkgs/main::ca-certificates-2020.1.1-0 --> conda-forge::ca-certificates-2020.4.5.2-hecda079_0
certifi pkgs/main::certifi-2020.4.5.1-py37_0 --> conda-forge::certifi-2020.4.5.2-py37hc8dfbb8_0
conda pkgs/main::conda-4.8.3-py37_0 --> conda-forge::conda-4.8.3-py37hc8dfbb8_1
The following packages will be SUPERSEDED by a higher-priority channel:
openssl pkgs/main --> conda-forge
Proceed ([y]/n)? y
Downloading and Extracting Packages
openmp-5.0.0 | 576 KB | ############################################################################ | 100%
clangdev-5.0.0 | 189.0 MB | ############################################################################ | 100%
certifi-2020.4.5.2 | 152 KB | ############################################################################ | 100%
ca-certificates-2020 | 184 KB | ############################################################################ | 100%
python_abi-3.7 | 4 KB | ############################################################################ | 100%
libcblas-3.8.0 | 88 KB | ############################################################################ | 100%
conda-4.8.3 | 3.1 MB | ############################################################################ | 100%
liblapack-3.8.0 | 2.7 MB | ############################################################################ | 100%
control-0.8.3 | 350 KB | ############################################################################ | 100%
slycot-0.4.0.0 | 1.2 MB | ############################################################################ | 100%
libblas-3.8.0 | 188 KB | ############################################################################ | 100%
libflang-5.0.0 | 519 KB | ############################################################################ | 100%
Preparing transaction: done
Verifying transaction: done
Executing transaction: doneコード例
from control import matlab # MATLAB互換モジュールの読み込み
import numpy as np # 数値計算モジュールの読み込み
from matplotlib import pyplot as plt # グラフ描画モジュールの読み込み
sys1 = matlab.tf([0, 0, 1], [0.1, 0.1, 1.0]) # 伝達関数の設定(分子、分母多項式)
y1, t1 = matlab.step(sys1, T = np.arange(0, 10, 0.01)) # ステップ応答の算出(t=0~10)
plt.plot(t1, y1) # 応答描画
bd = matlab.bode(sys1) # ボード線図の描画
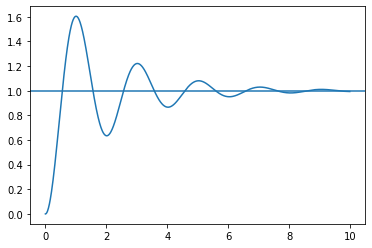
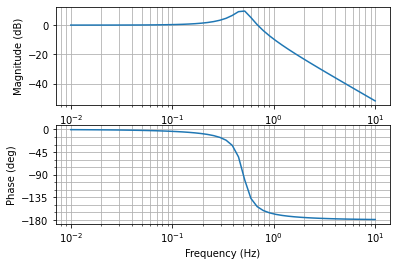
リンク
対数は「底$x$の値を何乗したら$z$になるか?」の指数を求めるもの、指定するものと捉える。
$z=x^y$での$y$を知りたい場合に$y=\log_{x}z$と書く。
常用対数は、対数の底が10のもの。
(※自然対数は対数の底がeのもの。${\rm e}^x$は微分しても${\rm e}^x$のままなので便利)
$\log_{10} 1 = 0, (10^0=1)$
$\log_{10} 2 \fallingdotseq 0.3$
$\log_{10} 2^{10}=\log_{10} 1024\fallingdotseq \log_{10} 1000=\log_{10}10^3=3\log_{10}10=3\cdot 1=3$
$\Rightarrow 10\log_{10}2\fallingdotseq3 \Rightarrow \log_{10}2\fallingdotseq \displaystyle\frac{3}{10}=0.3$
$\log_{10}3\fallingdotseq 0.475, (10^{0.5}=\sqrt{10}\fallingdotseq \sqrt{9}=3)$
$\log_{10}3^4=\log_{10}(9\cdot 9)=\log_{10}{81}\fallingdotseq \log_{10}80=\log_{10}(2^3\cdot 10) \Rightarrow 3\log_{10}2 + \log_{10}10 \fallingdotseq 3\cdot 0.3 + 1 = 1.9$
$\Rightarrow 4\log_{10}3\fallingdotseq 1.9 \Rightarrow \log_{10}3\fallingdotseq\displaystyle\frac{1.9}{4}=0.475$
$\log_{10}4\fallingdotseq 0.6$
$\log_{10}4=\log_{10}2^2=2\log_{10}2\fallingdotseq 2\cdot0.3=0.6$
$\log_{10}5\fallingdotseq 0.7$
$\log_{10}5=\log_{10}\displaystyle\frac{10}{2}=\log_{10}10-\log_{10}2\fallingdotseq 1-0.3 = 0.7$
$\log_{10}6\fallingdotseq 0.775$
$\log_{10}6=\log_{10}(2\cdot 3)=\log_{10}2 + \log_{10}3\fallingdotseq 0.3 + 0.475 = 0.775$
$\log_{10}7=0.85$
$\log_{10}7^2=\log_{10}49\fallingdotseq \log_{10}50 = \log_{10}(5\cdot10) = \log_{10}5+\log_{10}10\fallingdotseq 0.7+1$
$\Rightarrow 2\log_{10}7\fallingdotseq 1.7 \Rightarrow \log_{10}7\fallingdotseq \displaystyle\frac{1.7}{2}=0.85$
高精度版)
$\log_{10}7^4=\log_{10}2401\fallingdotseq \log_{10}2400 = \log_{10}(24\cdot100) = \log_{10}8+\log_{10}3+\log_{10}100$
$=\log_{10}2^3+\log_{10}3+\log_{10}10^2=3\log_{10}2+\log_{10}3+2\log_{10}10\fallingdotseq 3\cdot 0.3 + 0.475 + 2\cdot 1.0=3.375$
$\Rightarrow4\log_{10}7=3.375\Rightarrow\log_{10}7\fallingdotseq 3.375/4=0.84375\fallingdotseq 0.844$
$\log_{10}8\fallingdotseq 0.9$
$\log_{10}8=\log_{10}2^3=3\log_{10}2\fallingdotseq 3\cdot 0.3 = 0.9$
$\log_{10}9\fallingdotseq 0.95$
$\log_{10}9=\log_{10}3^2=2\log_{10}3\fallingdotseq 2\cdot 0.475=0.95$
高精度版)
$\log_{10}9^7=\log_{10}4782969\fallingdotseq \log_{10} 4800000 = \log_{10} (6\cdot 8\cdot 10^5) = \log_{10} 6 + \log_{10} 8 + \log_{10} 10^5$
$= 0.775 + 0.9 + 5.0=6.675$
$\Rightarrow 7\log_{10}9=6.675 \Rightarrow \log_{10}9 \fallingdotseq 6.675/7=0.9537\cdots\fallingdotseq 0.954$
$\log_{10}10=1, (10^1=10)$
おまけ:$\log_{10}11\fallingdotseq 1.04$
$\log_{10}11^5=\log_{10}161051\fallingdotseq \log_{10}160000=\log_{10}2^4\cdot10^4=4(\log_{10}2+\log_{10}10)\fallingdotseq 4(0.3+1.0)$
$\Rightarrow 5\log_{10}11=4\cdot1.3\Rightarrow \log_{10}11\fallingdotseq \displaystyle\frac{4}{5}1.3=0.8\cdot 1.3=1.04$
この近似をプロットすると下図のようになる。$\log_{10}7$と$\log_{10}9$は他に比べて誤差が大きいので、高精度版を赤色として示した。

|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 近似値 |
0 |
0.3 |
0.475 |
0.6 |
0.7 |
0.775 |
0.85 |
0.9 |
0.95 |
1 |
| 真値 |
0.000 |
0.3010 |
0.4771 |
0.6021 |
0.6990 |
0.7782 |
0.8451 |
0.9031 |
0.9542 |
1.000 |
| 誤差 |
0 |
0.0010 |
0.0021 |
0.0021 |
0.0010 |
0.0032 |
0.0049 |
0.0031 |
0.0042 |
0 |
観察
- 1~10で、$\log_{10}$は0~1になる。
- 3で$\log_{10}$は約0.45で、ざっくり半分に到達する。
- 2は$\log_{10}$は約0.3で、$4=2^2$, $8=2^3$だと$\log_{10}$はそれぞれ2,3倍の約0.6,0.9となる。8の際に既にほぼ1に近いことに注意。
- 5は10/2で、$\log_{10}$は$1-\log_{10}2$となるので約0.7。1と10の両端側からの距離でいうと2の場合と同じで約0.3。
- 倍になると、対数では同じだけ増加する。
例)
$\log_{10}2=0.3\stackrel{\times 2}{\longrightarrow}\log_{10}4=0.6\stackrel{\times 2}{\longrightarrow}\log_{10}8=0.9$,
$\log_{10}3=0.475\stackrel{\times 3}{\longrightarrow}\log_{10}9=0.95$,
$\log_{10}5=0.7\stackrel{\times 2}{\longrightarrow}\log_{10}10=1.0$
$\log aM=\log a + \log M$より、$a$倍されていれば、$\log a$分だけ増加する(割れば$\log a$だけ減少する)。$\rightarrow$掛け算・割り算が同じ距離の変化になる。
-
2で割ると$\log_{10}$では0.3減少するので、これを用いると
$\log_{10}3/2(=\log_{10}1.5)\fallingdotseq 0.475-0.3=0.175$
$\log_{10}5/2(=\log_{10}2.5)\fallingdotseq 0.7-0.3=0.4$
$\log_{10}7/2(=\log_{10}3.5)\fallingdotseq 0.85-0.3=0.55$
$\log_{10}9/2(=\log_{10}4.5)\fallingdotseq 0.95-0.3=0.65$
となる。1/2も求めてみると、
$\log_{10}1/2(=\log_{10}0.5)\fallingdotseq 0-0.3=-0.3$
となる。
$\log_{10}0.5=\log_{10}\displaystyle\frac{5}{10}=\log_{10}5-\log_{10}10\fallingdotseq 0.7-1=-0.3$
でも結果は同様。
参考リンク
2020年6月18日 in
未分類 | tags:
常用対数 |
No Comments
新型コロナウィルスの対応で会議や講義にZoomを使うことになってきたが、そのままだと部屋が映り込みまくる。
バーチャル背景の機能も優秀でスクリーンなしでも背景を置き換えてくれるようだが、そのままだと元から用意されている背景画像が、宇宙やらビーチやら壮大、軽快過ぎてちょっと会議等の状況にそぐわない。
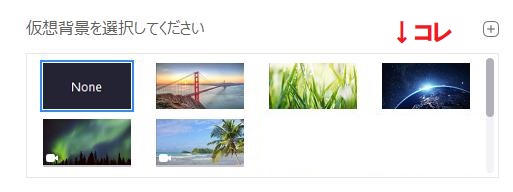
単なる単色も用意しておいてくれたらよかったが、それはないのでいくつか自前で作成することにした。
とはいえ、単なる単色だけだと味気ないので、ほんのりグラデーションを入れた。左側を少し明るめで右側を暗めにするほうがいいみたい。







グラデーション生成にはInkscapeを使った。
バーチャル背景の設定は、画面上部右端のプロフィールボタンから、設定⇒バーチャル背景と選び、任意の画像を指定する。
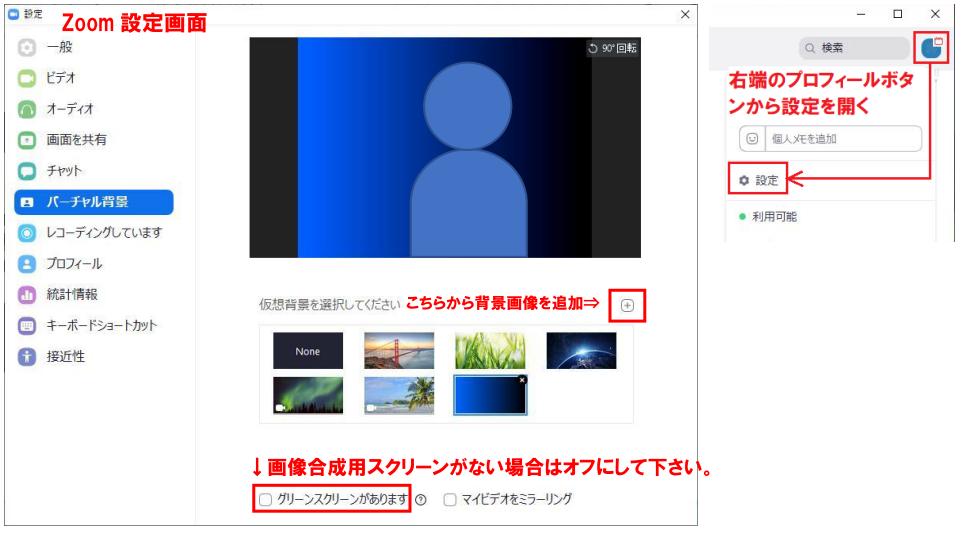
このとき、設定下部の「グリーンスクリーンがあります。」がオンとなっていると、合成用のスクリーンがある前提での動作になってしまうので、スクリーンを使わない場合はこれは外しておく。
Zoomは脆弱性等が問題山積みになっているようだが、今のところ一択ツール。なんとか修正・改善されて無事に使えますように…。
どこまで使い物になるか不明だが、同種のオープンソースツールもある。
あと、Zoomの紹介動画をいくつか。
前にハガキに印刷しようとしていて、普通紙を使ってまずはテストをしようと、A4用紙を折って切っていったらだいたいそれっぽいサイズになったのだが、微妙に違う。
A4用紙の折り方か、切り方を間違えたのかと思ったが、やっぱり違う。
調べるとA4を2回半分にしたA6用紙のサイズは105x148mmで、ハガキは100x148mmだった。この5mmの違いは何!?
と思ったのだが、ハガキのサイズは万国共通(万国郵便連合)で決まっているとのこと。
サイズを入れた比較図をパワポでのマウス操作で作ってもみたが、どうせならと手入力SVGで作成してみた。

ほぼ、単に四角を2つ並べるだけだから(初心者でも)簡単だろうと思ったらけっこう手こずったわ…。(かくして、この記事に続く…⇒MDN文書の翻訳)
[おまけ]
あと、WordPressにSVGをアップロードしようとしたらセキュリティ関連で蹴られて、プラグインを入れて対応した。プラグインは探すといくつか出てきたのだが、とりあえずSVG Supportを入れてみた。
2020年4月3日 in
未分類 | tags:
A6,
SVG,
ハガキ |
1 Comment
SVGで簡単な図形を描こうとしていたら、思いのほか手こずってMDNの翻訳作業にまでたどり着いてしまった。
翻訳作業をしやすくするユーザスクリプトがあって、基本単語の自動翻訳(置換)などを自動化してくれるらしく、FirefoxでもTampermonkey1) を使えばインストールできて動作ししそうな記述があるのだが、インストールはできて英語版のリビジョン取得くらいはできるのだが、バージョンが古くなってしまったのか、Firefoxへの対応がうまくいっていないのか動作しないみたい。
1) これまで「Tempermonkey」かと思っていたが、「Tamper(改ざん)monkey」だった。
MDN文書には EmbedLiveSample のしくみがあって、スクリプトの動作例を埋め込めて、実際に多数の動作例が既に存在しているのだが、そのサンプルのBlockIDに相当する<h2>タグなどのidがサイト側への保存時に勝手に翻訳したタイトルに合わせて日本語になってしまうので、これに(アドホックに)対処するには現状ではname属性も併記することしかないらしい。(もちろん、日本語に書き換えられたhタグのidに合わせてライブサンプルのBlockIDも日本語にしても動作するが、統一性がなくなるのでよくないですな。)
上記した翻訳援助スクリプトだと、このnameタグ付けも自動化する機能があるようだが、残念ながら動作しなかった。
あと、MDNでのブラウザ上のエディタだと「自動保存しました」などと出てくるが、その保存データの復帰方法が分からない。うっかり別ページを表示させたりすると、それまで作業していたデータが消えてなくなってイチからの作業し直しになってしまう。かといって、毎回保存してしまうと、保存のたびにリビジョンが増えるしその状況で公開状態になってしまう。GitHubも関連している風なのだが、自前保存で作業しておき、ある段階でまとめて更新とかできんのか?
細かいリビジョンが多数発生した際に、ひとまとめにできないかとも問い合わせてみたが、そういう機能はないとのことだった。
2020年3月29日 in
未分類 | tags:
MDN,
SVG |
No Comments










